【报资讯】数学文化论文3000字左右_数学文化论文3000字
1、数学作为一种文化现象,早已是人们的常识。
 (资料图片仅供参考)
(资料图片仅供参考)
2、历史地看,古希腊和文艺复兴时期的文化名人,往往本身就是数学家。
3、最著名的如柏拉图和达·芬奇。
4、晚近以来,爱因斯坦、希尔伯特、罗素、冯·诺依曼等文化名人也都是20世纪数学文明的缔造者。
5、 数学文化的存在价值 在即将公布的高中数学课程标准中,数学文化是一个单独的板块,给予了特别的重视。
6、许多老师会问为什么要这样做?一个重要的原因是,20世纪初年的数学曾经存在着脱离社会文化的孤立主义倾向,并一直影响到今天的中国。
7、数学的过度形式化,使人错误地感到数学只是少数天才脑子里想象出来的“自由创造物”,数学的发展无须社会的推动,其真理性无须实践的检验,当然,数学的进步也无须人类文化的哺育。
8、于是,西方的数学界有“经验主义的复兴”。
9、怀特(L.A.White)的数学文化论力图把数学回归到文化层面。
10、克莱因(M.Kline)的《古今数学思想》、《西方文化中的数学》、《数学:确定性的丧失》相继问世,力图营造数学文化的人文色彩。
11、 国内最早注意数学文化的学者是北京大学的教授孙小礼,她和邓东皋等合编的《数学与文化》,汇集了一些数学名家的有关论述,也记录了从自然辩证法研究的角度对数学文化的思考。
12、稍后出版的有齐民友的《数学与文化》,主要从非欧几何产生的历史阐述数学的文化价值,特别指出了数学思维的文化意义。
13、郑毓信等出版的专著《数学文化学》,特点是用社会建构主义的哲学观,强调“数学共同体”产生的文化效应。
14、 以上的著作以及许多的论文,都力图把数学从单纯的逻辑演绎推理的圈子中解放出来,重点是分析数学文明史,充分揭示数学的文化内涵,肯定数学作为文化存在的价值。
15、 认识和实施数学文化教育 进入21世纪之后,数学文化的研究更加深入。
16、一个重要的标志是数学文化走进中小学课堂,渗入实际数学教学,努力使学生在学习数学过程中真正受到文化感染,产生文化共鸣,体会数学的文化品位,体察社会文化和数学文化之间的互动。
17、 那么,如何在中小学数学教学中进行数学文化教育呢?笔者认为应该从以下几个方面加以认识和实施。
18、 认识数学文化的民族性和世界性 每个民族都有自己的文化,也就一定有属于这个文化的数学。
19、古希腊的数学和中国传统数学都有辉煌的成就、优秀的传统。
20、但是,它们之间有着明显的差异。
21、古希腊和古代中国的不同政治文明孕育了不同的数学。
22、 古希腊是奴隶制国家。
23、当时希腊的雅典城邦实行奴隶主的民主政治(广大奴隶不能享受这种民主)。
24、男性奴隶主的全体大会选举执政官,对一些战争、财政大事实行民主表决。
25、这种政治文明包含着某些合理的因素。
26、奴隶主之间讲民主,往往需要用理由说服对方,使学术上的辩论风气浓厚。
27、为了证明自己坚持的是真理,也就需要证明。
28、先设一些人人皆同意的“公理”,规定一些名词的意义,然后把要陈述的命题,称为公理的逻辑推论。
29、欧氏的《几何原本》正是在这样的背景下产生的。
30、 中国在春秋战国时期也有百家争鸣的学术风气,但是没有实行古希腊统治者之间的民主政治,而是实行君王统治制度。
31、春秋战国时期,也是知识分子自由表达见解的黄金年代。
32、当时的思想家和数学家,主要目标是帮助君王统治臣民、管理国家。
33、因此,中国的古代数学,多半以“管理数学”的形式出现,目的是为了丈量田亩、兴修水利、分配劳力、计算税收、运输粮食等国家管理的实用目标。
34、理性探讨在这里退居其次。
35、因此,从文化意义上看,中国数学可以说是“管理数学”和“木匠数学”,存在的形式则是官方的文书。
36、 古希腊的文化时尚,是追求精神上享受,以获得对大自然的理解为最高目标。
37、因此,“对顶角相等”这样的命题,在《几何原本》里列入命题15,借助公理3(等量减等量,其差相等)给予证明。
38、在中国的数学文化里,不可能给这样的直观命题留下位置。
39、 同样,中国数学强调实用的管理数学,却在算法上得到了长足的发展。
40、负数的运用、解方程的开根法,以及杨辉(贾宪)三角、祖冲之的圆周率计算、天元术那样的精致计算课题,也只能在中国诞生,而为古希腊文明所轻视。
41、 我们应当充分重视中国传统数学中的实用与算法的传统,同时又必须吸收人类一切有益的数学文化创造,包括古希腊的文化传统。
42、当进入21世纪的时候,我们作为地球村的村民,一定要溶入世界数学文化,将民族性和世界性有机地结合起来。
43、 揭示数学文化内涵,走出数学孤立主义的阴影 数学的内涵十分丰富。
44、但在中国数学教育界,常常有“数学=逻辑”的观念。
45、据调查,学生们把数学看作“一堆绝对真理的总集”,或者是“一种符号的游戏”。
46、“数学遵循记忆事实-运用算法-执行记忆得来的公式-算出答案”的模式[1],“数学=逻辑”的公式带来了许多负面影响。
47、正如一位智者所说,一个充满活力的数学美女,只剩下一副X光照片上的骨架了! 数学的内涵,包括用数学的观点观察现实,构造数学模型,学习数学的语言、图表、符号表示,进行数学交流。
48、通过理性思维,培养严谨素质,追求创新精神,欣赏数学之美。
49、 和所有文化现象一样,数学文化直接支配着人们的行动。
50、孤立主义的数学文化,一方面拒人于千里之外,使人望数学而生畏;另一方面,又孤芳自赏,自言自语,令人把数学家当成“怪人”。
51、学校里的数学,原本是青少年喜爱的学科,却成为过滤的“筛子”、打人的“棒子”。
52、优秀的数学文化,会是美丽动人的数学王后、得心应手的仆人、聪明伶俐的宠物。
53、伴随着先进的数学文化,数学教学会变得生气勃勃、有血有肉、光彩照人。
54、 多侧面地开展数学文化研究 谈到数学文化,往往会联想到数学史。
55、确实,宏观地观察数学,从历史上考察数学的进步,确实是揭示数学文化层面的重要途径。
56、但是,除了这种宏观的历史考察之外,还应该有微观的一面,即从具体的数学概念、数学方法、数学思想中揭示数学的文化底蕴。
57、以下将阐述一些新视角,力求多侧面地展现数学文化。
58、 1. 数学和文学。
59、数学和文学的思考方法往往是相通的。
60、举例来说,中学课程里有“对称”,文学中则有“对仗”。
61、对称是一种变换,变过去了却有些性质保持不变。
62、轴对称,即是依对称轴对折,图形的形状和大小都保持不变。
63、那么对仗是什么?无非是上联变成下联,但是字词句的某些特性不变。
64、王维诗云:“明月松间照,清泉石上流”。
65、这里,明月对清泉,都是自然景物,没有变。
66、形容词“明”对“清”,名词“月”对“泉”,词性不变。
67、其余各词均如此。
68、变化中的不变性质,在文化中、文学中、数学中,都广泛存在着。
69、数学中的“对偶理论”,拓扑学的变与不变,都是这种思想的体现。
70、文学意境也有和数学观念相通的地方。
71、徐利治先生早就指出:“孤帆远影碧空尽”,正是极限概念的意境。
72、 2.欧氏几何和中国古代的时空观。
73、初唐诗人陈子昂有句云:“前不见古人,后不见来者,念天地之悠悠,独怆然而涕下。
74、”这是时间和三维欧几里得空间的文学描述。
75、在陈子昂看来,时间是两头无限的,以他自己为原点,恰可比喻为一条直线。
76、天是平面,地是平面,人类生活在这悠远而空旷的时空里,不禁感慨万千。
77、数学正是把这种人生感受精确化、形式化。
78、诗人的想象可以补充我们的数学理解。
79、 3. 数学与语言。
80、语言是文化的载体和外壳。
81、数学的一种文化表现形式,就是把数学溶入语言之中。
82、“不管三七二十一”涉及乘法口诀,“三下二除五就把它解决了”则是算盘口诀。
83、再如“万无一失”,在中国语言里比喻“有绝对把握”,但是,这句成语可以联系“小概率事件”进行思考。
84、“十万有一失”在航天器的零件中也是不允许的。
85、此外,“指数爆炸”“直线上升”等等已经进入日常语言。
86、它们的含义可与事物的复杂性相联系(计算复杂性问题),正是所需要研究的。
87、“事业坐标”“人生轨迹”也已经是人们耳熟能详的词语。
88、 4. 数学的宏观和微观认识。
89、宏观和微观是从物理学借用过来的,后来变成一种常识性的名词。
90、以函数为例,初中和高中的函数概念有变量说和对应说之分,其实是宏观描述和微观刻画的区别。
91、初中的变量说,实际上是宏观观察,主要考察它的变化趋势和性态。
92、高中的对应则是微观的分析。
93、在分段函数的端点处,函数值在这一段,还是下一段,差一点都不行。
94、政治上有全局和局部,物理上有牛顿力学与量子力学,电影中有全景和细部,国画中有泼墨山水画和工笔花鸟画,其道理都是一样的。
95、是否要从这样的观点考察函数呢? 5. 数学和美学。
96、“1/2+1/3=2/5 ?”是不是和谐美?二次方程的求根公式美不美?这涉及到美学观。
97、三角函数课堂上应该提到音乐,立体几何课总得说说绘画,如何把立体的图形画在平面上。
98、欣赏艾舍尔(M.C.Escher)的画、计算机画出的分形图,也是数学美的表现。
本文就为大家分享到这里,希望小伙伴们会喜欢。
标签:
下一篇:最后一页
- 焦点消息!GPLP投融资:摩尔线程获15亿元 奔腾激光获1.7亿元
- 世界快消息!吃西瓜怎么保存不坏 西瓜怎么保存比较好
- 热点聚焦:一波N折 糖价明年有点看头
- 每日速递:声迅股份:发行可转债2.80亿元 申购日为12月30日
- 环球新动态:生意宝12月27日涨停分析
- 天天速读:日本强降雪致多人死伤 局地积雪厚度超1.6米
- 【世界播资讯】俄罗斯政府将拨款约15亿卢布用于国产飞机研发制造
- 环球百事通!最近头发老是掉,一抓一大把,这该怎么办呢?
- 当前聚焦:永清环保新余垃圾发电厂获2022年度新余市科技计划项目立项支持
- 当前热讯:调查:当年英国“脱欧”支持者中仅约三成认为“脱欧”成功
- 每日快讯!四位明星的家人因新冠去世!谢晋儿子抢救无效,樊登父亲安详离世
- 观速讯丨四高校花费超千万采购核酸检测服务,有供应商仅6人参保
- 每日快播:东方锆业“产能利用率”存疑:加码电熔氧化锆前景堪忧
- 【环球新要闻】重量天花板体验新标杆 OPPO Find N2上手评测
- 当前聚焦:新疆塔什库尔干机场正式通航 帕米尔高原喜迎“空中来客”
- 世界播报:大连合同纠纷律师收费标准
- 环球今头条!犀牛看市1220:大盘全天低开低走 汽车板块午后反弹
- 天天亮点!如何主动投资为插上量化翅膀?长盛基金王宁不喧哗自有声
- 当前关注:表面是百亿票房先生,实际全是“水货”,求求这几位演员别尬吹了
- 世界热门:上坤地产(06900.HK)再度大幅走强,尾盘升约45%
- 新动态:市场先生大变脸
- 快看点丨2023年初级会计师考试采取什么考试方式
- 全球快资讯:首钢股份董秘回复:长流程钢铁生产与短流程钢铁生产或是您提到的单工序生产都有各自的特点
- 今日关注:微软发现苹果 macOS 漏洞,可植入恶意软件
- 当前短讯!芳源股份: 独立董事关于第三届董事会第十二次会议相关事项的事前认可意见
- 每日速递:小鲨易贷逾期九年多久会上征信
- 焦点快报!【机构调研记录】长安基金调研浙海德曼
- 世界百事通!漳州龙海交警严查电动车非法加装挡风披
- 世界快看点丨犀牛宝逾期十二个月影响征信吗
- 全球聚焦:先行先试为企减负 反哺创新初显成效
- 全球热议:海航科技(600751):海航科技股份有限公司关于资产购买的进展公告
- 【快播报】2022年中国货车细分市场供需情况 轻型货车销量最高【组图】
- 天天视讯!【机构调研记录】金信基金调研福田汽车
- 全球热点评!辖区居民面包车被盗 濮阳华龙公安迅速出击
- 聚焦:尔康制药:对氨基苯酚目前满负荷生产
- 天天时讯:禾丰股份:12月14日融券卖出金额21.77万元,占当日流出金额的0.48%
- 今日最新!鑫铂股份(003038.SZ)1415.73万股限售股将于12月16日上市流通
- 环球热讯:西上海:如有重大事项,公司将依法依规进行信息披露
- 环球热点!12月13日基金净值:广发均衡增长混合A最新净值0.9697,跌0.26%
- 天天快播:黄山旅游(600054)12月13日主力资金净买入1515.54万元
- 【世界独家】南京化纤:截止2022年12月09日,公司股东人数为24223人
- 全球快看:斯迪克获3家机构调研:公司生产的OCA,应用场景非常广泛,除了应用在手机终端以外,还可以用在可穿戴设备等小尺寸的屏幕上(附调研问答)
- 天天通讯!沙棘的种植方法 沙棘树怎么种
- 重点聚焦!华通线缆: 河北华通线缆集团股份有限公司股东大会议事规则(2022年12月修订)
- 今热点:招商港口: 第十届董事会2022年度第十次临时会议决议公告
- 今日关注:南阳市镇平县:“五个一”开展网格化管理
- 世界信息:天沃科技董秘回复:感谢您对天沃科技的关心和支持!公司未开展虚拟电厂相关业务
- 深圳证券交易所2022年会员大会召开 提升服务实体经济能力
- 合肥举行“江淮普法行”活动 营造高质量法治环境
- 纸浆期货是否有效对冲废黄板纸现货价格波动风险?
-
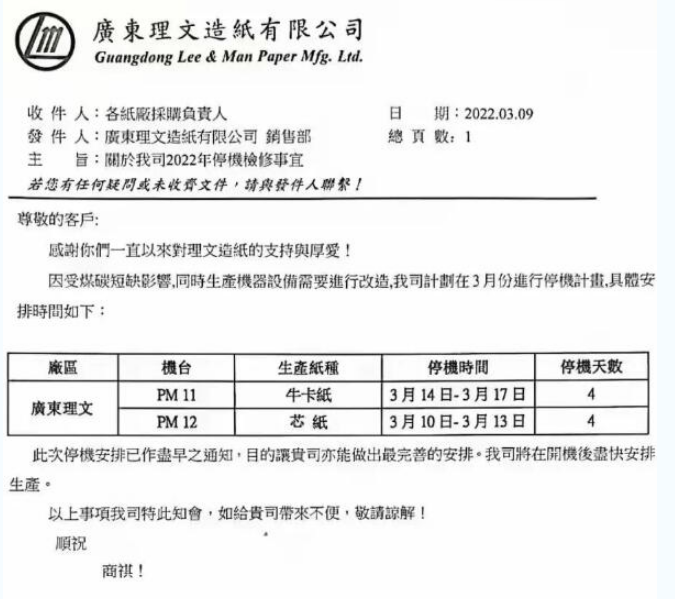
理文、山鹰发布停机函 包装纸市场涨价100-200元/吨
3月初,市场依然低迷!没想到即将步入中旬,市场却开始停机函、涨价函齐飞……这波操作会激起水花吗?3月9...
-

全部合格!广东珠海抽查5批次油墨产品
2021年第三季度,珠海市市场监督管理局组织开展了油墨产品质量监督抽查。本次共抽查了1家企业生产的5批...
-

浆系纸种再掀新一轮提价 涨幅达200-1500元/吨
继2月份多纸种接棒提价发起春季涨价攻势后,3月1日起,浆系纸种再掀新一轮的密集提价,涉及文化纸、白卡...
-

保定满城区开展纸制品行业专项检查 规范纸制品企业生产
为进一步规范纸制品企业生产经营行为,提升纸制品产业质量总体水平,近日,保定市满城区市场监督管理局...
-

2022年3月14日全国各地区纸厂废纸价格信息
华北地区:河北唐山乐亭张氏纸业,上调50元 吨。河北秦皇岛昌黎兴昌纸业,上调30元 吨。河北秦皇岛金...
-

包装材料、人工费等成本上升 台湾生活用纸涨价
由于原材料、物流、能源、环保以及包装材料、人工费等成本不断上升,台湾生活用纸生产企业已难以承受,...
-

上周木浆系纸品价格均有提涨 箱板纸价小幅下跌
本周轻工制造行业指数下跌4 57%, 跑输大盘0 35pct;造纸子板块下跌3 57%,跑赢大盘0 66pct 本周沪...
-

景兴纸业2021年营收同比增27.70% 净利同比增41.51%
3月14日,景兴纸业(002067)发布2021年度业绩快报公告,公告显示,2021年1-12月营业总收入为6,224,614,59...
-

1-2月全国快递业务收入1574.3亿 同比增长13.8%
3月14日,国家邮政局公布2022年2月邮政行业运行情况。数据显示,1-2月,全国快递服务企业业务量累计完成...
-

原料成本压力持续上升 浙江多家包装厂产品价格上涨3%
3月15日,多份包装企业涨价函从浙江嘉兴、湖州等地传来。在这些涨价函中,包装企业普遍表示,受疫情影响...
-

3月7日-13日生活用纸主要区域市场周度价格情况
上周(3月7—3月13日),河北、湖北、川渝、广西等生活用纸主要生产区域,纸浆及生活用纸市场价格情况汇总...
-

安徽出台“十四五”大气污染防治规划
安徽省生态环境厅日前印发《安徽省十四五大气污染防治规划》(以下简称《规划》)。《规划》要求,到2025...
-

原材料/燃料价格上涨 日本卫生纸、纸尿裤提价超10%
由于纸浆和能源等原材料 燃料价格上涨,物流成本、劳动力成本攀升以及环境措施成本增加,日本各造纸企...
-

新加坡超市将对塑料袋收费 至少5分新币/个
近日,永续发展与环境部长傅海燕在国会上宣布,从明年中旬起,三分之二新加坡超市都开始对一次性购物袋...
-

电子商务兴起 印度纸类包装行业发展趋势
随着市场越来越倾向于可持续性包装解决方案,预计未来几年对纸质包装的整体需求将增加。可持续性概念为...
-

2022年1-2月芬兰木材交易同比下滑20%
2022年1-2月,芬兰森林工业协会会员企业从私人森林采购木材累计达420万立方米,比去年同期下降20%。纸浆...
-

山东造纸行业深入实施“链长制”工作推进机制
造纸业作为基础原材料工业,在国民经济中占据重要地位。2021年,山东全省造纸行业深入实施链长制工作推...
-

包装原料价格波动再成热点 揭秘2021造纸上市企业业绩
近日,包装原料的价格波动再度成为热点,从废纸到原纸、到纸板,都传出了价格异动的消息。同时,在过去...
-

国家统计局:1-2月规上工业增加值同比实际增长7.5%
3月15日,国家统计局发布了2022年1-2月份工业生产主要数据。同日,国家统计局工业司副司长汤魏巍就1-2月...
-

2022年3月18日各地区各大纸厂废纸价格信息
华北地区:河北秦皇岛昌黎兴昌纸业,上调30元 吨。内蒙古昭宣纸业,下调20-30元 吨。华中地区:河南新...
-

江苏开展精准造林绿化 深入推进国土绿化和全民义务植树
江苏省今年着力实施精准绿化造林,深入推进国土绿化和全民义务植树。全省计划造林绿化20万亩,建设绿美...
-

正隆纸业员工返岗率超95% 预计今年营收同比增10%
人勤春来早,奋进正当时。位于厚街镇桥头第四工业区的正隆(广东)纸业有限公司(以下简称正隆纸业)自大年...
-

芬林芬宝劳马新锯材厂将启用自动装载生产线
芬林芬宝位于芬兰劳马的新锯材厂即将启用的自动装载生产线开创了锯材行业内的先河。自动装载指的是在无...
-

山东一小镇发展纸箱包装生产企业近百家 年产值11亿元
在山东省聊城市冠县北馆陶镇,返乡创业的孙凤湘在自家院子里把纸箱加工事业做得红红火火。他透露:从大...
-
打破性别“玻璃天花板” 95岁女院士是“她力量”最佳代言
鼓励女性打破“玻璃天花板” 95岁女院士就是“她力量”最佳代言 打破性别“玻璃天花板”,锤子...
-
河北辛集市暂停举办体育活动 关闭景区文娱场所
今天(11月8日)上午,河北省辛集市召开疫情防控新闻发布会,通报当地疫情防控最新情况。辛集市文体局...
-
红色文物·党史故事 “推出胜利”的小推车
“推出胜利”的小推车 李晓莉 在淮海战役纪念馆中,有一辆小推车格外引人注目,它就是淮海...
-
侵华日军南京大屠杀遇难同胞纪念馆闭馆
中新网南京11月8日电(记者 申冉)8日,侵华日军南京大屠杀遇难同胞纪念馆通报,该馆定于2021年11月1...
-
核酸采样:一位“点长”的50小时冲刺
11月4日晚上9点过,巴南区桥南社区盛世江南小区临时核酸采样点,市第七人民医院眼耳鼻喉科护士长张...
-
跑道结冰 哈尔滨机场关闭至9日12时
中新网哈尔滨11月8日电 (仇建 记者 史轶夫)哈尔滨太平国际机场8日发布消息,因跑道结冰,该机场...
-
北京地铁全面开启车内加热装置
地铁全面开启车内加热装置 本报讯(记者 李博)为做好降雪和强降温天气的应对工作,北京地铁合理...
-
黑河市多举措保障疫情期间残疾人等特殊群体生活稳定
中新网黑河11月8日电 (记者 史轶夫 王琳)8日,黑河市新冠肺炎疫情防控工作第十五场新闻发布会召...
-
北京丰台海淀两处管控区域解封 社区工作者收到“暖心礼物”
丰台海淀两处管控区域解封 居民和社区工作者收到“暖心礼物” 本报记者 孙颖 于丽爽 昨...
-
吉林四平一旅游项目违占耕地两千多亩 投资达10亿元
吉林四平一旅游项目违占两千多亩耕地被通报,投资达10亿元 近日,自然资源部通报了29宗农村乱占...
-
湖南双峰27名非法滞留缅北人员被惩戒:小孩回原籍入学
湖南双峰籍27名非法滞留缅北人员被惩戒:其小孩一律回原籍入学 为打击跨境电信诈骗犯罪,全国多...
-
江西新增本土“1+6” 上饶增一中风险地区
(抗击新冠肺炎)江西新增本土“1+6” 上饶增一中风险地区 中新网南昌11月8日电 (记者 吴鹏泉)...
-
江西上饶一地调整为中风险地区 实行封闭管理措施
中新网11月8日电 据江西省上饶市政府新闻办公室官方微博消息,上饶市新冠疫情防控应急指挥部8日发...
-
快递旺季遭遇雨雪天气 国家邮政局呼吁理解快递小哥
快递旺季遭遇雨雪天气 国家邮政局呼吁多理解和包容快递小哥 本报北京11月7日电(记者甘皙)国家...
-
高压、孤独,胆大、心细:手执焊枪的水下“蛙人”
高压、湿冷、孤独,胆大、心细、技艺高超—— 手执焊枪的水下“蛙人” 早上6时,伴随初升的朝...
-
掏粪掏了36年,他还在琢磨“新门道”
优化清掏路线、干活做到“三净”、总结技术诀窍,清掏工苏广林—— 掏粪掏了36年,他还在琢磨“...
-
内蒙古:二连浩特市新增1例本土确诊病例 额济纳旗累计治愈出院本土确诊病例76例
(抗击新冠肺炎)内蒙古:二连浩特市新增1例本土确诊病例 额济纳旗累计治愈出院本土确诊病例76例 ...
-
坚守在海拔4300多米的“天路保健医生”
中新网拉萨11月8日电(贡嘎来松)5日,青藏铁路格尔木至拉萨段达琼果站,海拔4327米。中铁十二局集团...
-
38年后,他终于知道了家在哪儿……
“我是谁,多大了,家在哪儿?”38年来,他总有这样一个心结被死死凝结,总为这样一句疑问而苦苦追...
-
受降雪影响 辽宁鞍山一农贸市场发生坍塌
8日早上6时左右,受连续强降雪影响,辽宁省鞍山市千山区大屯镇农贸市场发生坍塌,多台车辆被砸。 ...
-
中国舞蹈家协会顶尖教师巡回课堂(重庆站)举办
中新网北京11月8日电 (记者 高凯)由中国舞蹈家协会主办,中国文联舞蹈艺术中心、重庆市舞蹈家协会...
-
边城战“疫”:夜晚七点的暂停键
11月4日晚上7点,是中俄边境城市黑河一个再平凡不过的抗疫时刻。 如果在这一刻按下时间的暂停键...
-
风雪高原战“疫”长卷 寒潮下的西宁疫情防控观察
大风7级,大雪纷扬,最高气温只有-5℃! 这是青海省西宁市开启全城全员首轮核酸检测的天气。 ...
-
拟音师:“雕刻”声音的人【三百六十行】
三百六十行 拟音师:“雕刻”声音的人 闭上眼,90后赵洪泽有时甚至可以通过走路的声音,来判...
-
“双减”之后 中小学教师资格考试为何依然火爆
聚焦 “双减”之后,中小学教师资格考试为何依然火爆 近日,2021年下半年中小学教师资格考试(...
-
大数据助力贫困生成长
探索 大数据助力贫困生成长大数据画像能为贫困生成长带来什么 今年9月,云南省楚雄彝族自治州...
X 关闭
X 关闭